You know the right answer? Which ordered pair makes both inequalities true? y < -x + 1. y > x.(x, y) can take integer values from 1 onwards since they must be positive integers. x and y can each increase by 1 and the sum will stay less than 10. (x, y) = (1, 2), (2, 1), The moment (x, y) becomes (2, 2), the sum becomes 10 which is not acceptable.Find an answer to your question ✅ "Which ordered pair makes both inequalities true Yx" in Mathematics if you're in doubt about the correctness of the answers or there's no answer, then try to use the smart search and find answers to the similar questions.In electronic communication system, digital signalsa. do not provide a continuous set of values.b. represent values as discrete steps.c. utilize binary system.d. utilize decimal as well as binary systems.Which of the above statements are true ?Answer OptionsWait does that make sense to you. The answer is A (-1,-5) y=x-4 -5= -1-4 Hope it make and that was a fake ms.sue. Similar Questions. Math. which ordered pair is a solution of the inequality y≥4x - 5 (3,4) (2,1) (3,0) (1,1). The coordinates of an ordered pair have opposite signs.
How many ordered pairs of positive integers (x,y) satisfy the inequali
Replace in the inequality with the second value in the ordered pair. Do the indicated arithmetic. Examine the result: If you have true statement, then the ordered pair is an element of the solution set of the inequality.an ordered pair that makes both equations true. You will find a y and that pair (x,y) is an ordered pair that is a solution to this equation. For example, let x=0 Then we have -5y=-1so y=1/5 The ordered pair (0, 1/5) is a point on the line and a solution to the equation.To find: Ordered pair which makes he inequalities true. Pair 3: x = -1 , y = -3. Inequality (1)Which ordered pair makes both inequalities true? A. y > 1/3x + 3 and 3x - y > 2. Which system of linear inequalities is represented by the graph?

Which ordered pair makes both inequalities true Y<-x+1 Y>x
For ordered pair (-2,2), as 2>-2 so it is true for y>x. ordered pair (-2,2) is true for both inequalities.answers to question: Which ordered pair makes both inequalities true? y < -x + 1 y > x On a coordinate plane, 2 straight lines are shown. The first solid line has a negative slope and goes through (0, 1) and (1, 0). Everything below an - on study-assistant.com.None of these ordered pairs make both inequalities true. Step-by-step explanation: The given inequalities are. Ellen makes and sells bookmarks. she graphs the number of bookmarks sold compared to the total money earned. why is the rate of change for the function graphed to the left?Ordered pair: In the set theory, we learnt to write a set in different forms, we also learnt about different types of sets and studied operations on sets and Venn diagrams. Two ordered pairs (a, b) and (c, d) are equal if a = c and b = d, i.e., (a, b) = (c, d). Find the values of x and y, if (2x - 3, y + 1) = (x + 5, 7).We need to find the ordered pair which makes both inequalities true. Check the above inequalities for each given ordered pair. So, both inequalities are true for (-2,2). Option B is correct.
(*1*)Hi Nicole,
(*1*)y<-x+1 y>x (*1*) for ordered pair (-3,5), as 5>-3, so it's true for y>x (*1*) 5>-(-3)+1 or 5>4 so it's now not true for y<-x+1 (*1*) For ordered pair (-2,2), as 2>-2 so it's true for y>x (*1*) 2 <-(-2)+1 or 2<3 so it is true for y<-x+1 (*1*) for ordered pair (-1,-3), -3 <-1 so it isn't true for y>x (*1*) (0,-1) , -1<0 so it is not true for y>x (*1*)ordered pair (-2,2) is true for both inequalities.Which Ordered Pairs Make Both Inequalities True? Check All

6.6 Solving System Of Linear Inequalities: - [PPTX Powerpoint]
![6.6 Solving System Of Linear Inequalities: - [PPTX Powerpoint] 6.6 Solving System Of Linear Inequalities: - [PPTX Powerpoint]](https://i0.wp.com/reader012.vdocuments.mx/reader012/slide/20171212/56816297550346895dd30e4b/document-18.png?t=1606573780)
Graphing Systems Of Inequalities
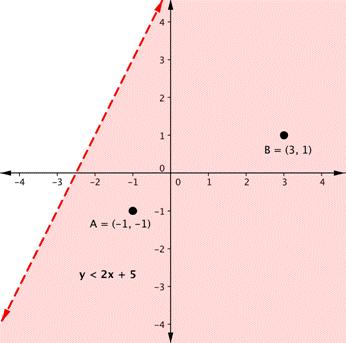
Which Ordered Pair Makes Both Inequalities True? Y > –3x

Which Is True About The Solution To The System Of

Which Ordered Pair Makes Both Inequalities True? Y X

How Do You Tell Whether The Ordered Pair (2,5) Is A

Question 2.2. Which Ordered Pairs Make The Inequality True

[Solved] Which Ordered Pair Makes Both Inequalities True
![[Solved] Which Ordered Pair Makes Both Inequalities True [Solved] Which Ordered Pair Makes Both Inequalities True](https://i0.wp.com/us-static.z-dn.net/files/d1e/6621f47434672e37d84da202a9478798.png)
HELP PLEASE I WILL GIVE BRAINLIEST AND 35 POINTS

Which Ordered Pair Makes Both Inequalities True? Y X On A
Which System Of Linear Inequalities Has The Point (3,2) In

Determine If The Ordered Pair (6, 4) Is A Solution To The

Which Ordered Pair Makes Both Inequalities True? Y X (–3

Which Ordered Pair Makes Both Inequalities True? Y

PPT - 6.6 Solving System Of Linear Inequalities
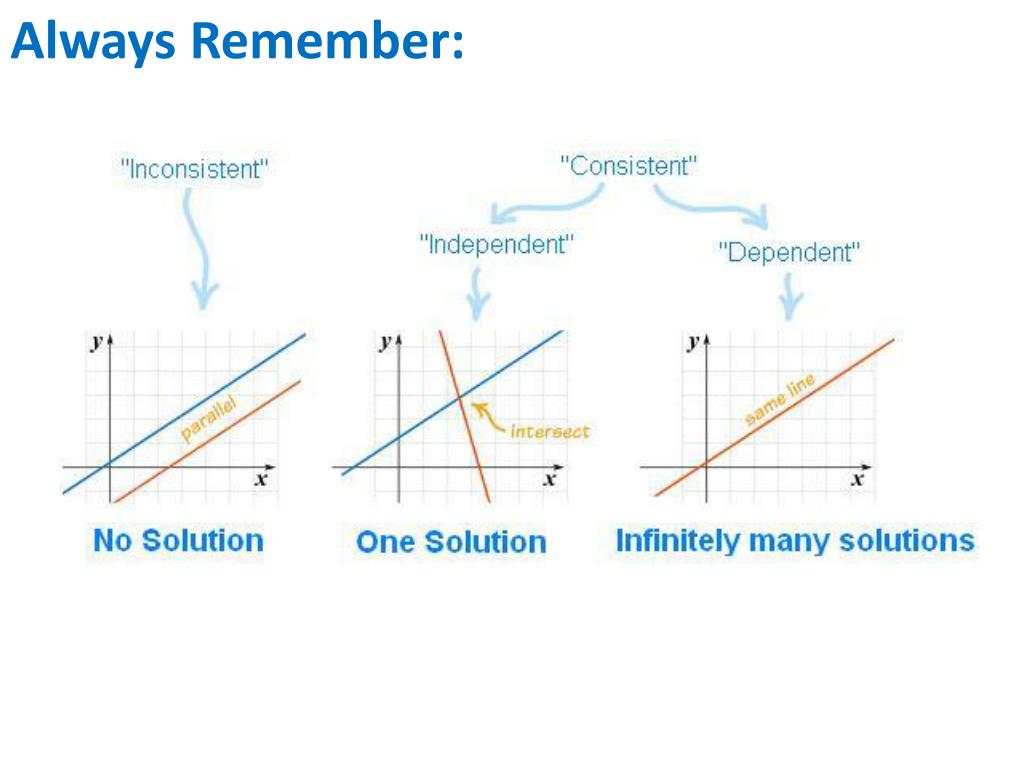
Which Ordered Pairs Make Both Inequalities True? Check All

Solve Systems Of Linear Equations With Two Variables

Systems Of Equations

Which Ordered Pair Makes Both Inequalities True? Y > –3x

Which Of The Ordered Pairs In The Form (x, Y) Is A

0 comments:
Post a Comment